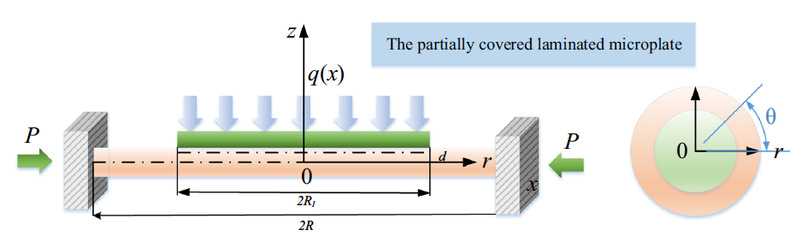
Our centre lecturer Guangyang Fu publised academical paper “On the size-dependent bending and buckling of the partially covered laminated microplate” at the international journal ENGINEERING WITH COMPUTERS (Q2, TOP journal, IF: 8.083, Journal number: 0177-0667).
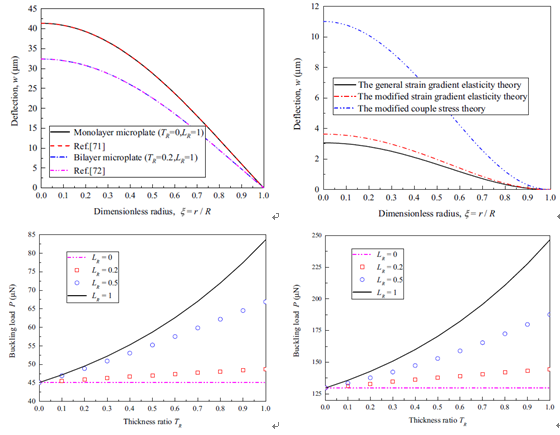
A size-dependent model for a laminated microbeam with a partially covered flexoelectric layer is developed by using the isotropic flexoelectric theory. The static bending problem of the beam under the uniformly distributed load and the voltage with different boundary conditions is solved. The method of weighted residuals is applied to derive the analytical expressions of the charge, the potential, the polarization and the deflection. The size dependency of the charge, the potential, the polarization and the deflection is discussed. Results reveal that the charge, the potential, the polarization and the deflection is dependent on the ratio of beam thickness and material length-scale parameters. As the ratio increases, the charge, the potential, the polarization and the deflection gradually increase. In addition, the effects of length and thickness of flexoelectric layer on the induced charge and induced deflection are also studied. There is an optimum length and thickness of the flexoelectric layer to achieve the maximum induced charge and maximum induced deflection.
Equilibrium equation and Boundary conditions:
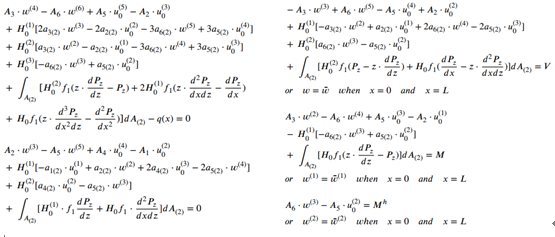
Results reveal that the collected charge, the polarization, the electric potential and the deflection generated from the flexoelectric process show obviously size effects. The collected charge, the polarization the electric potential and the deflection gradually decrease with the decrease of the ratio of the beam thickness to the material length scale parameter. In addition, the effects of length and thickness of the flexoelectric layer on the flexoelectric response of the beam is dependent on the combined influences from the external load, equivalent moment and the bending rigidity. An increase in the length of the flexoelectric layer leads to the collected charge and the induced deflection of the clamped-clamped beam first increase and then decrease. When the thickness ratio is taken as 1, length ratio is taken as 0.66, the induced charge generated from the direct flexoelectric effects reaches the peak. When the thickness ratio is taken as 1, length ratio is taken as 0.54, the induced deflection generated from the inverse flexoelectric effects reaches the peak.