Our centre Dr. FU Guangyang publised academical paper “On the strain gradient effects on buckling of the partially covered laminated microbeam” at the TOP journal Applied Mathematical Modelling. The corresponding author is Professor ZHENG Hongyu.
Introduction:
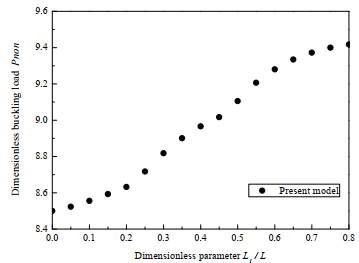
In this paper, we derive the theoretical relations among the classical couple stress theory, the modified couple stress theory and the general theory. The general theory includes all strain gradients and can respectively reduce to the classical couple stress theory and the modified couple stress theory when certain strain gradients are ignored. Subsequently, we further compare the difference of the ability of the general theory and the reduced theories to capture the size-dependent buckling response of the beam. The buckling load of the beam predicted by the general theory is larger than that predicted by the reduced theories. The general theory can predict the size dependency more accurately. In addition, the variation law of buckling load with the location of the upper elastic layer is also clarified. The location variation of the upper elastic layer leads to the change of buckling load, and thus affects the ability of the beam to resist the deformation.
Laminated microbeam:

Non-laminated region Equilibrium equation:
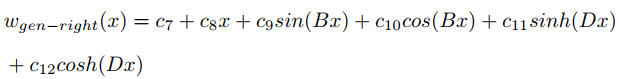
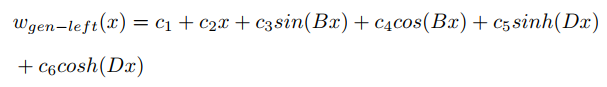
Laminated region Equilibrium equation:
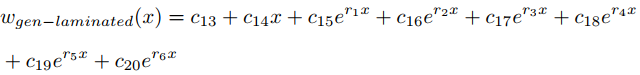
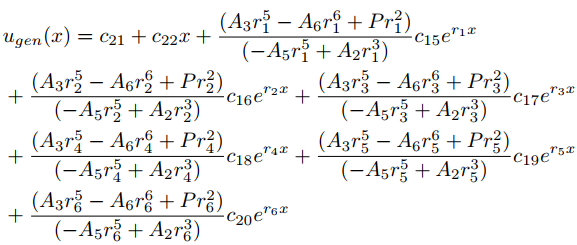
Results and Discussion:
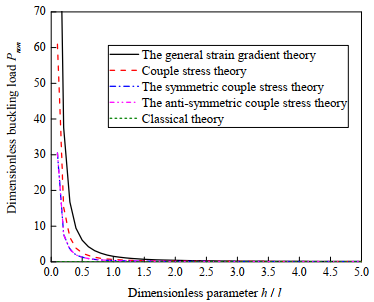
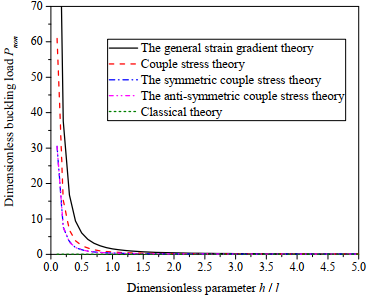

In this paper, the relations and differences among the anti-symmetric couple stress theory, the symmetric couple stress theory, the classical couple stress theory and the general theory are discussed. The anti-symmetric/symmetric couple stress theory and the classical couple stress theory are the reduced theory of the general theory. Then, the size dependency of buckling response of partially covered laminated microbeam is analysed. The expression of the buckling load of the beam is derived. The influences from material parameters and the laminated location on the buckling load are discussed.
Results reveal that as the ratio of the thickness and length parameter increases, the dimensionless buckling load subsequently decreases, and thus shows obviously size effects. Compared with the general theory, the reduced theories predict smaller buckling load, and underestimate the size effects. The dilatation gradients has predominate effects on the buckling response compared with the rotation gradients and the stretch gradients. In addition, the relation among the length, thickness, location of the upper elastic layer and the buckling load is also studied. The buckling load increases gradually with the increase of thickness and length of the upper elastic layer. The ability of the beam to resist the deformation is dependent on the location of the upper elastic layer and the boundary conditions.


